Serrio Mal
Visualizing the Mandelbrot Set as a 3D polygon mesh.

~ 2 min read

The Mandelbulb

Visualizing the Mandelbrot Set as a 3D polygon mesh.

  • blender
  • generative art
  • rendering

The Mandelbrot Set is a set of complex numbers CC where fC(Z)=Z2+Cf_C (Z) = Z^2 + C does not diverge towards infinity, instead staying bounded. The set is the 2D plane of valid permutations.

The Mandelbulb is a 3D spherical representation of the 2D Mandelbrot set, and is iterated with the formula:

Zn+1=ZnP+CZ_{n+1} = Z_n^{P} + C

Where:

  • ZZ is the current (x, y, z) position tuple
  • CC is a triplex value, initialized to the current position tuple
  • EXPEXP is a constant exponent value, e.g. 88

There’s a few variations of the formula out on the web, but the implementation that yielded good results for me here was:

len=Zx2+Zy2+Zz2θ=arcsin⁡(Zzlen)⋅EXPϕ=arctan⁡(Zy,Zx)⋅EXPρ=lenEXP⋅len\begin{align} len &= \sqrt{Z_x^2 + Z_y^2 + Z_z^2}\\ \theta &= \arcsin(\frac{Z_z}{len}) \cdot EXP\\ \phi &= \arctan(Z_y, Z_x) \cdot EXP\\ \rho &= len^{EXP} \cdot len\\ \end{align}

The new (x, y, z) coordinates for Zn+1Z_{n+1} are provided by:

x′=cos⁡(ϕ)⋅cos⁡(θ)⋅ρy′=sin⁡(ϕ)⋅cos⁡(θ)⋅ρz′=sin⁡(θ)⋅ρZn+1=(x′,y′,z′)+C\begin{align} x' &= \cos(\phi) \cdot \cos(\theta) \cdot \rho \\ y' &= \sin(\phi) \cdot \cos(\theta) \cdot \rho \\ z' &= \sin(\theta) \cdot \rho \\ Z_{n+1} = (x', y', z') + C \end{align}

Recursively iterating over the coordinates will create a point cloud which can then be visualized in software such as Processing, Blender or Houdini. Blender 3.3’s Geometry Nodes now has a Volume to Mesh node, which allows you to convert the result into a point mesh geometry.

Mandelbulb front view Mandelbulb front view
Mandelbulb profile view Mandelbulb profile view
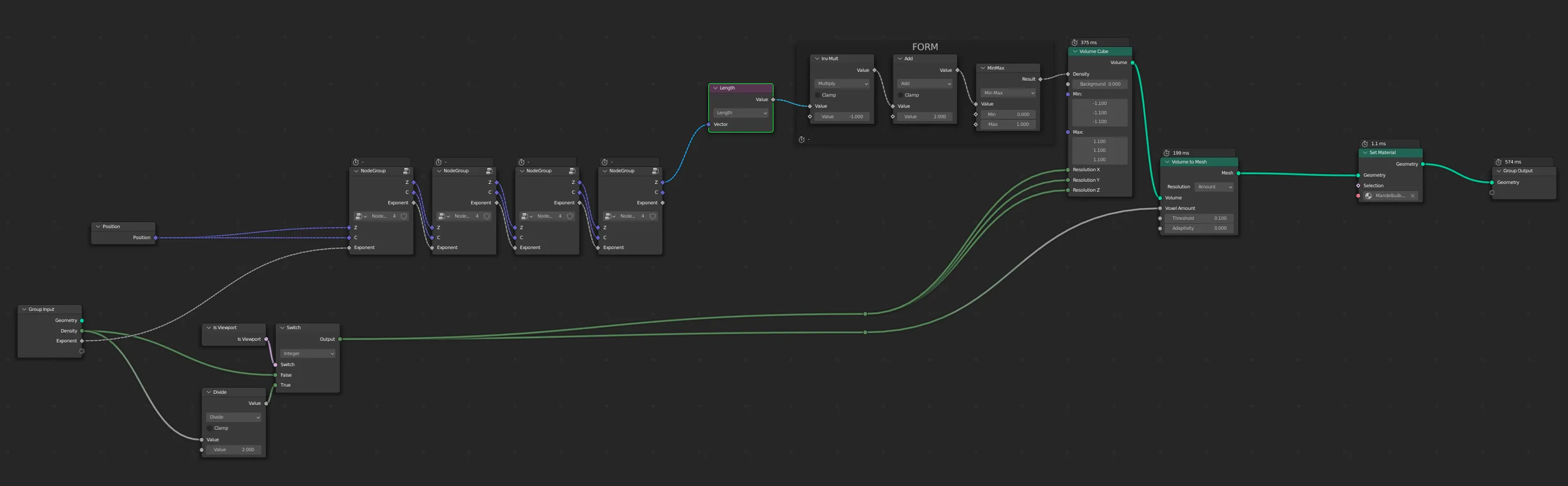
Mandelbulb nodes layout Mandelbulb nodes layout

Geometry Nodes layout

References